Integral Tentu-Konsep Luas

'DEMI KENYAMANAN PEMBACA! SEBELUM MEMBACA DISARANKAN UNTUK MENGGUNAKAN MODE DESKTOP BAGI PARA PENGGUNA MOBILE! DIKARENAKAN BEBERAPA SUSUNAN KATA AKAN BERHAMBURAN PADA MODE MOBILE'

Integral tentu (definite integral) adalah integral yang memiliki batas-batas nilai tertentu, sehingga hasil akhirnya bisa ditentukan secara pasti. Batas-batas nilai itu merupakan nilai variabel dari fungsi yang telah diintegralkan. Sebelumnya kita telah mempelajari notasi sigma, pada materi kali ini kita akan kita akan membahas mengenai Integral tentu pada konsep luas. Dua konsep paling berpengaruh dalam kalkulus berasal dari dua isu, yang keduanya bersifat geometris. Masalah pertama dengan garis singgung memperkenalkan ide turunan, sedangkan masalah kedua dengan luas memperkenalkan ide integral tertentu. Kami akan berkonsentrasi pada masalah kedua.

Dalam matematika dasar di bangku sekolah menengah anda harusnya telah diperkenalkan sedikit tentang konsep integral dan bagaimana menghitung luas. Dengan menggunakan rumus baku yang telah diberikan saat itu, anda sekarang harusnya dapat menghitung luas suatu persegi panjang, segitiga, maupun jajaran genjang dengan sangat mudah. Kita tidak akan mengulangnya lagi di sini, tetapi kita akan lebih memfokuskan bagaimana konsep integral ini membawa kita kepada masalah mengenai suatu luas daerah dengan batas yang melengkung.

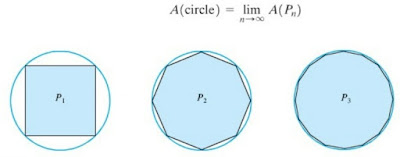
Bilamana kita meninjau suatu daerah dengan batas melengkung, masalah penentuan luas menjadi lebih sukar. Tetapi lebih dari 2000 tahun yang silam, Archimedes telah menyediakan kunci untuk suatu penyelesaian. Katanya, pandang satu barisan poligon dalam (poligonnya berada dalam suatu lingkaran) yang menghampiri daerah melengkung dengan kecermatan yang semakin besar (Gambar 1).

Sebagai contoh, untuk lingkaran radius 1, pandang poligon dalam beraturan $P 1, P 2, P 3, \dots$ $P1,P2,P3,…$ dengan 4 sisi, 8 sisi, 16 sisi, limit untuk $n \to \infty$ $n→∞$ dari luas-luas $P_{n}$ $P_n$ . Jadi, jika $A (F)$ $A(F)$ menyatakan luas suatu daerah F, maka.

Gambar 1

Archimedes juga melanjutkan bahwa dengan memandang poligon-poligon luar (poligonnya berada di luar suatu lingkaran) $T_{1}, T_{2}, T_{3}, ...$ $T_1,T_2,T_3,...$ (Gambar 2), kita akan memperoleh nilai yang sama untuk luas lingkaran radius 1 ( yaitu, $π \approx 3, 14159$ $π≈3,14159$ ) tidak peduli apakah anda memakai poligon dalam atau poligon luar.

Gambar 2

Sekarang mari kita bahas lebih mendetail apa yang telah dimaksudkan di atas.

Luas Menurut Poligon-Poligon Dalam

Pandang daerah R yang dibatasi oleh parabol $y = f (x) = x^{2}$ $y=f(x)=x^2$ , sumbu-x, dan garis tegak $x = 2$ $x = 2$ (Gambar 3). Kita acu R sebagai daerah di bawah kurva $y = x^{2}$ $y=x^2$ di antara $x = 0$ $x = 0$ dan $x = 2$ $x=2$ . Tujuan kita adalah menghitung luas $A (R)$ $A(R)$ .

Gambar 3

Gambar 4

Pastikan (seperti pada Gambar 4) selang $[0, 2]$ $[0,2]$ menjadi $n$ $n$ selang bagian, masing-masing dengan panjang $x = \frac{2}{n}$ $x=2 / n$ , memakai titik-titik.

$0 = x_{0} < x_{1} < x_{2} < \dots < x_{n - 1} < x_{n} = 2$ $0=x_0<x_1<x_2<\cdots<x_{n-1}<x_n=2$

Jadi,

$x_{0} = 0$ $x_0 =0$

$x_{1} = Δ x = \frac{2}{n}$ $x_1 =\Delta x=\frac{2}{n}$

$x_{2} = 2 \cdot Δ x = \frac{4}{n}$ $x_2 =2 \cdot \Delta x=\frac{4}{n}$

$⋮$ $\vdots$

$x_{i} = i \cdot Δ x = \frac{2 i}{n}$ $x_i =i \cdot \Delta x=\frac{2 i}{n}$

$⋮$ $\vdots$

$x_{n - 1} = (n - 1) \cdot Δ x = \frac{(n - 1) 2}{n}$ $x_{n-1} =(n-1) \cdot \Delta x=\frac{(n-1) 2}{n}$

$x_{n} = n \cdot Δ x = n (\frac{2}{n}) = 2$ $x_n =n \cdot \Delta x=n\left(\frac{2}{n}\right)=2$

Pandang persegi-panjang dengan alas $[x_{1-1}, x_i]$ dan tinggi $f(x_{i-1}) = x_{i-1}^2$ . Luasnya adalah $f(x_{i-1})Δx$ (lihat bagian kiri dari Gambar 6). Gabungan $R_n$ dari semua persegi-panjang yang demikian membentuk poligon dalam yang diperlihatkan pada bagian kanan dari Gambar 5.

Gambar 5

Luas $A\left(R_n\right)$ dapat dihitung

$A\left(R_n\right)=f\left(x_0\right) \Delta x+f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\cdots+f\left(x_{n-1}\right) \Delta x$

Sekarang,

$f\left(x_i\right) \Delta x=x_i^2 \Delta x=\left(\frac{2 i}{n}\right)^2 \cdot \frac{2}{n}=\left(\frac{8}{n^3}\right) i^2$

Jadi,

$A\left(R_n\right)$ $=\left[\frac{8}{n^3}\left(0^2\right)+\frac{8}{n^3}\left(1^2\right)+\frac{8}{n^3}\left(2^2\right)+\cdots+\frac{8}{n^3}(n-1)^2\right]$

$=_{n^3}^8\left[1^2+2^2+\cdots+(n-1)^2\right]$

$=\frac{8}{n^3}\left[\frac{(n-1) n(2 n-1)}{6}\right]$

$\text { Rumus } 2 \text { Jumlah Khusus, }$

$\text { dengan } \ n-1 \text { menggantikan } \ n$

$=\frac{8}{6}\left(\frac{2 n^3-3 n^2+n}{n^3}\right)$

$=\frac{4}{3}\left(2-\frac{3}{n}+\frac{1}{n^2}\right)$

$=\frac{8}{3}-\frac{4}{n}+\frac{4}{3 n^2}$

Kita simpulkan bahwa

$A(R)=\lim _{n \rightarrow \infty} A\left(R_n\right)=\lim _{n \rightarrow \infty}\left(\frac{8}{3}-\frac{4}{n}+\frac{4}{3 n^2}\right)=\frac{8}{3}$

Diagram-diagram pada Gambar 6 akan membantu anda membayangkan apa yang terjadi bilamana $n$ semakin membesar. Jika $n$ semakin besar mendekati takhingga maka luas dari seluruh poligon akan sama dengan luas daerah $R$ .

Gambar 6

Contoh

Hitunglah luas poligon yang dibatasi oleh kurva $y=1 / 2 x$ , sumbu $x$ , garis $x=2$ dan $x=4$ , jika daerah poligon tersebut dibagi atas 5 poligon bagian yang sama.

Jawab :

Karena selang $[2,5]$ dipartisi atas 5 selang bagian yang sama, maka $\Delta x=(4-2) / 5=2 / 5$ , dan

$x_{0}=2$

$x_{1}=2+1 \Delta x=2+2 / 5=12 / 5$

$x_{2}=2+2 \Delta x=2+4 / 5=14 / 5$

$x_{3}=2+3 \Delta x=2+6 / 5=16 / 5$

$x_{4}=2+4 \Delta x=2+8 / 5=18 / 5$

$x_{5}=2+5 \Delta x=2+10 / 5=4$

Luas poligon dalam :

$L\left(P_{dalam}\right) = f(x 0) \Delta x+f(x 1) \Delta x+f(x 3) \Delta x+f(x 4) \Delta x$

$=\left(\frac{1}{2}\right)(2)\left(\frac{2}{5}\right)+\left(\frac{1}{2}\right)\left(\frac{12}{5}\right)\left(\frac{2}{5}\right)+\left(\frac{1}{2}\right)\left(\frac{14}{5}\right)+\left(\frac{1}{2}\right)\left(\frac{16}{5}\right)\left(\frac{2}{5}\right)+\left(\frac{1}{2}\right)\left(\frac{18}{5}\right)\left(\frac{2}{5}\right)$

$=\left(\frac{12}{25}\right)+\left(\frac{14}{5}\right)+\left(\frac{18}{25}\right)+\left(\frac{18}{25}\right)+\left(\frac{20}{25}\right)$

$=\left(\frac{80}{25}\right)$

$=\left(\frac{16}{5}\right)$

Luas Menurut Poligon-Poligon Luar

Mungkin anda belum yakin bahwa $A(R)=8/3$ . Kita dapat memberikan lebih banyak fakta. Pandang persegi panjang dengan alas $[x_{i-1}, x_i]$ dan tinggi $f(x_i)=x_i^2$ (diperlihatkan pada bagian kiri Gambar 7). Luasnya adalah $f(x_i)Δx$ . Gabungan $S_n$ dari semua persegi panjang yang demikian membentuk suatu poligon luar untuk daerah $R$ , seperti diperlihatkan pada bagian kanan Gambr 7.

Gambar 7

Luas daerah $A\left(S_n\right)$ dihitung secara analog dengan perhitungan $A\left(R_n\right)$ .

$A\left(S_n\right)=f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\cdots+f\left(x_n\right) \Delta x$

Seperti sebelumnya, $f\left(x_i\right) \Delta x=x_i^2 \Delta x=\left(8 / n^3\right) i^2$ , sehingga

$A\left(S_n\right)$ $=\left[\frac{8}{n^3}\left(1^2\right)+\frac{8}{n^3}\left(2^2\right)+\cdots+\frac{8}{n^3}\left(n^2\right)\right]$

$=\frac{8}{n^3}\left[1^2+2^2+\cdots+n^2\right]$

$=\frac{8}{n^3}\left[\frac{n(n+1)(2 n+1)}{6}\right] \text { Rumus } 2 \text { Jumlah Khusus }$

$=\frac{8}{6}\left[\frac{2 n^3+3 n^2+n}{n^3}\right]$

$=\frac{8}{3}+\frac{4}{n}+\frac{4}{3 n^2}$

Sekali lagi, kita simpulkan bahwa

$A(R)=\lim _{n \rightarrow \infty} A\left(S_n\right)=\lim _{n \rightarrow \infty}\left(\frac{8}{3}+\frac{4}{n}+\frac{4}{3 n^2}\right)=\frac{8}{3}$

Contoh

Hitunglah jumlah Rieman $R_p$ untuk $f\left(x\right)=x-1$ Dan partisi P adalah $3<3,75<4,25<5,5<6<7$ serta titik-titik sampel: $x1=3,x2=4,x3=4.75,x4=6,danx5=6.75$

Jawab:

$R_p=\sum_{i=1}^5f\left(x_1\right)\triangle x$

$=(2)(0,75)+(3)(0,5)+(3,75)(1,25)+(5)(0,5)+(5,75)(1)$

$=15,9375$

ATAS KEKURANGANNYA MOHON DIMAAFKAN, AUTHOR MASIH DALAM TAHAP BELAJAR UNTUK MEMBUAT BLOG INI.

Tempat berbagi informasi seputar hal menarik

Integral Tentu-Konsep Luas

0 Response to "Integral Tentu-Konsep Luas"

Post a Comment

Artikel Populer

Kategori

Daftar Isi

Integral Tentu-Konsep Luas

Related Posts :

0 Response to "Integral Tentu-Konsep Luas"

Post a Comment